The transfer function of a DC servo motor represents the relationship between the motor’s input (typically voltage or current) and its output (usually speed or position) in the frequency domain. This mathematical model is critical for designing control systems that govern the motor’s behavior in various applications, such as robotics, CNC machines, and automotive systems.
The accuracy of the transfer function is influenced by several motor parameters, including resistance (R), inductance (L), and friction (b), which affect the dynamics of the motor’s response to inputs.
Comprehending a DC Servo Motor’s Transfer Function
Before diving into the influence of specific parameters, it is important to understand the basic structure of a DC servo motor’s transfer function. A typical DC motor consists of:
- Armature resistance (R): The resistance of the motor’s windings.
- Armature inductance (L): The inductance of the armature winding.
- Back electromotive force (EMF): The voltage generated by the motor’s rotation, opposing the input voltage.
- Motor inertia (J): The motor’s resistance to variations in rotational speed.
- Damping (b): The frictional forces opposing the motor’s rotation.
- Torque constant (K_T): The proportionality constant between the input current and the motor’s output torque.
- Back EMF constant (K_E): The proportionality constant between the motor speed and the back EMF generated.
A DC motor’s transfer function can be written as:
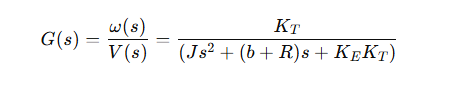
where:
- ω(s)\omega(s)ω(s) is the angular velocity of the motor (output),
- V(s)V(s)V(s) is the input voltage,
- sss is the complex frequency variable in the Laplace domain.
Effect of Resistance (R) on the Transfer Function
The resistance in the armature winding plays a significant role in determining the motor’s electrical time constant, which impacts both the transient and steady-state behavior of the motor. The resistance value directly affects the damping of the motor system and is embedded in the denominator of the transfer function. Specifically, resistance influences the following aspects of the motor’s behavior:
- Speed Response: Higher resistance leads to higher energy losses in the windings, resulting in slower acceleration and a less responsive motor. The increase in resistance can cause the system to become underdamped, with slower settling times.
- Power Consumption: Increased resistance results in higher power dissipation as heat, reducing the efficiency of the motor and increasing the system’s thermal load.
- Stability: Resistance is a crucial parameter in controlling the damping ratio of the motor. Higher resistance generally increases damping, improving stability but possibly reducing performance in high-speed applications.
In terms of the transfer function, resistance affects the pole locations in the system. As resistance increases, the damping factor becomes more significant, shifting the poles toward the left half of the complex plane, leading to a more stable but slower system.
Effect of Inductance (L) on the Transfer Function
Inductance in the armature winding governs the motor’s electrical time constant, which is determined by the relationship between inductance (L) and resistance (R). Inductance has several important effects on the transfer function and motor dynamics:
- Transient Response: High inductance slows down the system’s response to input changes, as it takes longer for the current to change due to the opposition created by the inductance. This means the motor will have a slower transient response, which could be problematic in high-performance applications requiring rapid acceleration.
- Overshoot and Settling Time: In systems with high inductance, the motor’s response may exhibit a longer rise time and larger overshoot before it reaches steady state. This is because the inductance resists changes in current, delaying the motor’s acceleration and deceleration.
- Steady-State Error: Inductance can contribute to a steady-state error if the system is poorly tuned, particularly in systems where velocity or position control is critical.
From a control system perspective, inductance modifies the poles of the system, causing them to move closer to the imaginary axis. This can lead to a slower response and, in some cases, cause the system to oscillate if not properly damped.
In the transfer function, inductance appears in the form of an LLL term in the numerator and denominator. This term significantly affects the time constant of the system and can alter the motor’s ability to track rapid changes in the input signal.
The Transfer Function and Friction (b)
Friction is an often overlooked but critical parameter in DC motors. It represents the mechanical resistance opposing the motion of the motor’s rotor and includes bearing friction, air resistance, and any other forms of mechanical losses. Friction primarily affects the motor’s damping and inertia terms, and its influence is seen in the following ways:
- System Damping: Friction adds to the overall damping of the motor system, increasing the speed at which the motor reaches its final position or speed. In many cases, increasing friction can improve the system’s stability by reducing oscillations or overshoot.
- Torque Loss: Friction introduces a constant torque opposing the motor’s rotation, which reduces the overall efficiency of the system. This torque loss can impact the motor’s ability to maintain high speeds or precise positioning over time.
- Position Control: In position-controlled applications, friction can introduce a static error or offset, as the motor must overcome the frictional forces to reach and maintain a set position.
In the transfer function, friction is typically modeled as part of the damping term. It impacts the system’s transient response as well as the actual component of the poles. Increased friction can lead to faster settling times but may also reduce the motor’s efficiency and increase wear and tear.
Variations in Motor Parameters and Their Effect on System Dynamics
A DC servo motor’s dynamic behavior, including reaction time, stability, and efficiency, is determined by the interplay of resistance, inductance, and friction.Small adjustments to any one of these factors can have a big impact on the motor’s performance.
- Increased Resistance: Leads to a reduction in speed, increased power loss, and a potential decrease in system efficiency. It also increases damping, which can affect transient performance.
- Increased Inductance: Causes slower response times and may result in more oscillatory behavior if not properly tuned. It increases the electrical time constant, slowing the motor’s ability to react to changes in the input.
- Increased Friction: While it may increase damping and improve stability, excessive friction leads to power loss and reduced efficiency, negatively affecting the motor’s overall performance.
These variations must be carefully considered during the design and tuning process to ensure that the motor delivers the desired performance while maintaining energy efficiency and system stability.
Methods for Parameter Estimation and System Identification
To accurately model and control a DC servo motor, it is essential to estimate the motor parameters (R, L, b) precisely. Several methods can be used for parameter estimation and system identification:
- Empirical Measurement: Direct measurement of motor parameters using test equipment such as a power supply, oscilloscope, or multimeter. For instance, resistance can be measured with a standard ohmmeter, and inductance can be measured using an LCR meter.
- Motor Testing and Response Analysis: Applying step inputs or sinusoidal inputs to the motor and measuring its output response can help identify parameters. By analyzing the motor’s speed, position, and current response, it is possible to estimate the values of R, L, and b using curve fitting techniques.
- System Identification Techniques: Techniques like least-squares estimation, Kalman filtering, and other optimization methods can be employed to estimate motor parameters based on experimental data. These techniques are especially helpful in complicated systems where it can be difficult to assess parameters directly.
The transfer function of a DC servo motor provides a crucial mathematical model for understanding and controlling motor behavior. The motor parameters—resistance, inductance, and friction—significantly influence the system’s dynamics and must be carefully considered in the design and control process by DC servo motor manufacturer.
